Sight reduction

Sight reduction is the process of deriving from a sight the information needed for establishing a line of position.

Sight is defined as the observation of the altitude, and sometimes also the azimuth, of a celestial body for a line of position; or the data obtained by such observation.^[1]

Nowadays sight reduction uses the equation of the circle of equal altitude to calculate the altitude of the celestial body,

and the azimuth Zn is obtained from Z by:

With the observed altitude Ho, Hc and Zn are the parameters of the Marcq St Hilaire intercept for the line of position:

Correction to the sextant altitude

Marcq St Hilaire intercept for the line of position

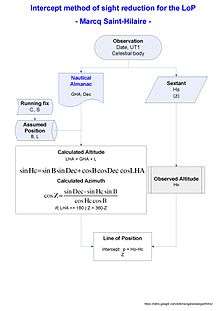
With B the latitude (+N/S), L the longitude (+E/-W), LHA = GHA + L is the local hour angle, Dec and GHA are the declination and Greenwich hour angle of the star observed, and Hc the calculated altitude. Z is the calculated azimuth of the body.

Basic procedures involved computer sight reduction or longhand tabular methods.

Tabular sight reduction

The methods included are:

• The Nautical Almanac Concise method (NASR)
• Pub. 249 (formerly H.O. 249, Sight Reduction Tables for Air Navigation, A.P. 3270 in the UK)
• Pub. 229 (formerly H.O. 229, Sight Reduction Tables for Marine Navigation
• H.D. 486 (in the United Kingdom)
• H.O. 214 (Tables of Computed Altitude and Azimuth)
• H.O. 211 (Dead Reckoning Altitude and Azimuth Table, Third Edition, known as Ageton, and the Modified H.O. 211 Compact Sight Reduction Table, known as Ageton-Bayless)
• H.O. 208 (Navigation Tables for Mariners and Aviators, Sixth Edition, known as Dreisonstok)
• S-Table

Longhand haversine sight reduction

This method is a practical procedure to reduce celestial sights with the needed accuracy, without using electronic tools such as calculator or a computer. And it could serve as a backup in case of malfunction of the positioning system aboard.

Doniol

The first approach of a compact and concise method was published by R. Doniol in 1955^[2] The altitude is derived from sin(Hc) = n − a (m + n), in which n = cos(B − Dec), m = cos(B + Dec), a = hav(LHA).

The calculation is:

n = cos(B - Dec)
m = cos(B + Dec)
a = hav(LHA)
sin_Hc = n - a (m + n)
Hc = arcsin(sin_Hc)

Ultra compact sight reduction

Haversine Sight Reduction algorithm

A practical and friendly method using haversines was developed between 2014 and 2015,^[3] and published in NavList.

A compact expression for the altitude was derived^[4] using haversines, hav, for all the terms of the equation:

hav(ZD) = hav(B - Dec) + (1 - hav(B - Dec) − hav(B + Dec)) hav(LHA)

where ZD is the zenith distance

Hc = (90 - ZD) the calculated altitude

The algorithm if absolute values are used is:

if same name for latitude and declination
 n = hav(|B| - |Dec|)
 m = hav(|B| + |Dec|)
if contrary name
 n = hav(|B| + |Dec|)
 m = hav(|B| - |Dec|)
q = n + m
a = hav(LHA)
hav(ZD) = n + (1 - q) a
ZD = invhav -> look at the haversine tables
Hc = 90° - ZD

For the azimuth a diagram^[5] was developed for a faster solution without calculation, and with an accuracy of 1°.

Azimuth diagram by Hanno Ix

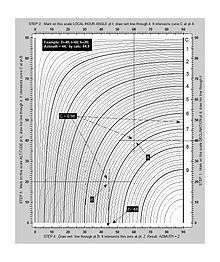
This diagram could be used also for star identification.^[6]

An ambiguity in the value of azimuth may arise since in the diagram 0 ≤ Z ≤ 90°. Z is E/W as the name of the meridian angle, but the N/S name is not determined. In most situations azimuth ambiguities are resolved simply by observation.

When there are reasons for doubt or for the purpose of checking the following formula^[7] should be used.

hav(Z) = [hav(90° - Dec) - hav(B - Hc)] / (1 - hav(B - Hc) - hav(B + Hc))

The algorithm if absolute values are used is:

if same name
 a = hav(90° - |Dec|)
if contrary name
 a = hav(90° + |Dec|)
m = hav(B + Hc)
n = hav(B - Hc)
q = n + m
hav(Z) = (a - n) / (1 - q)
Z = invhav -> look at the haversine tables
if Latitude N:
 if LHA > 180°, Zn = Z
 if LHA < 180°, Zn = 360° − Z
if Latitude S:
 if LHA > 180°, Zn = 180° − Z
 if LHA < 180°, Zn = 180° + Z

This computation of the altitude and the azimuth needs a haversine table. For a precision of 1 minute of arc, a four figure table is enough.^[8]

An example

Data:
 B = 34° 10.0′ N (+)
 Dec = 21° 11.0′ S (-)
 LHA = 302° 43.0′
Altitude Hc:
 a = 0.2298
 m = 0.0128
 n = 0.2157
 hav(ZD) = 0.3930 -> table ->
 ZD = 77° 39′
 Hc  = 12° 21′
Azimuth Zn:
 a = 0.6807
 m = 0.1560
 n = 0.0358
 hav(Z) = 0.7979
 Zn  = 126.6°

See also

• Navigation
• Celestial navigation
• Circle of equal altitude
• Intercept method

References

External links

• Navigational Algorithms: resources for Longhand Haversine Sight Reduction
• NavList A Community Devoted to the Preservation and Practice of Celestial Navigation and Other Methods of Traditional Position-Finding
• Celestial Tools for the USPS/CPS JN/N Student
• Graphical all-haversine Hc reduction