Single-valued function
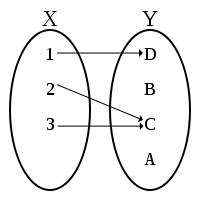
 . Each input, on the left, maps to a single output, on the right. This function is not injective, however, because two different numbers both map to the output "C"
. Each input, on the left, maps to a single output, on the right. This function is not injective, however, because two different numbers both map to the output "C"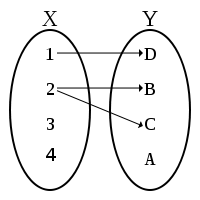
A single-valued function is an emphatic term for a mathematical function in the usual sense. That is, each element of the function's domain maps to a single, well-defined element of its range. This contrasts with a general binary relation, which can be viewed as being a multi-valued function.
Example
In complex analysis, each complex number other than 0 has three distinct cube roots. Therefore, the function f(z) = z1/3 can be naturally treated as a multi-valued function in which each number other than zero maps to three distinct values. The theory of Riemann surfaces gives a way to study the behavior of this function and other multi-valued functions on the complex numbers.
Injective functions
A function is injective (also called "one-to-one") if each element of the range arises from a single element of the domain. In contrast, a function is single-valued if each element of the domain maps to a single element of the range.
