Triangular function
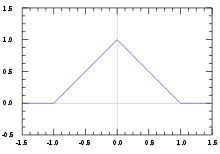
The triangular function (also known as the triangle function, hat function, or tent function) is defined either as:
or, equivalently, as the convolution of two identical unit rectangular functions:
The triangular function can also be represented as the product of the rectangular and absolute value functions:
The function is useful in signal processing and communication systems engineering as a representation of an idealized signal, and as a prototype or kernel from which more realistic signals can be derived. It also has applications in pulse code modulation as a pulse shape for transmitting digital signals and as a matched filter for receiving the signals. It is also equivalent to the triangular window sometimes called the Bartlett window.
Scaling
For any parameter, :
Fourier transform
The transform is easily determined using the convolution property of Fourier transforms and the Fourier transform of the rectangular function:
where is the normalized sinc function.
Extended version to repeat tent in all R domain
|(x mod 2)-1|
Alternative definition

Note that in some cases the triangle function may be defined to have a base of length 1 instead of length 2:
See also
- Tent map
- Triangular distribution
- Triangle wave, a piecewise linear periodic function