Yule–Simon distribution

Yule–Simon
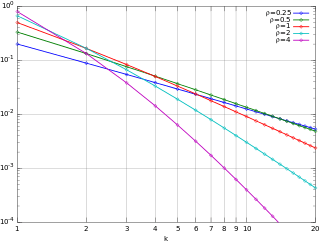
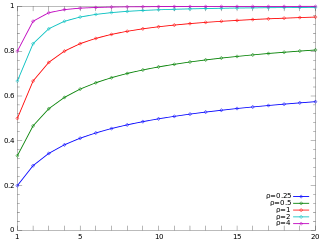
Probability mass function Yule–Simon PMF on a log-log scale. (Note that the function is only defined at integer values of k. The connecting lines do not indicate continuity.)
Cumulative distribution function Yule–Simon CMF. (Note that the function is only defined at integer values of k. The connecting lines do not indicate continuity.)
Parameters	$\rho >0\,$ shape (real)
Support	$k\in \{1,2,\dotsc \}$
pmf	$\rho \operatorname {B} (k,\rho +1)$
CDF	$1-k\operatorname {B} (k,\rho +1)$
Mean	${\frac {\rho }{\rho -1}}$ for $\rho >1$
Mode	$1$
Variance	${\frac {\rho ^{2}}{(\rho -1)^{2}(\rho -2)}}$ for $\rho >2$
Skewness	${\frac {(\rho +1)^{2}{\sqrt {\rho -2}}}{(\rho -3)\rho }}\,$ for $\rho >3$
Ex. kurtosis	$\rho +3+{\frac {11\rho ^{3}-49\rho -22}{(\rho -4)(\rho -3)\rho }}$ for $\rho >4$
MGF	${\frac {\rho }{\rho +1}}{}_{2}F_{1}(1,1;\rho +2;e^{t})\,e^{t}$
CF	${\frac {\rho }{\rho +1}}{}_{2}F_{1}(1,1;\rho +2;e^{i\,t})e^{i\,t}$

In probability and statistics, the Yule–Simon distribution is a discrete probability distribution named after Udny Yule and Herbert A. Simon. Simon originally called it the Yule distribution.^[1]

The probability mass function (pmf) of the Yule–Simon (ρ) distribution is

f(k;\rho )=\rho \operatorname {B} (k,\rho +1),

for integer $k\geq 1$ and real $\rho >0$ , where $\operatorname {B}$ is the beta function. Equivalently the pmf can be written in terms of the falling factorial as

f(k;\rho )={\frac {\rho \Gamma (\rho +1)}{(k+\rho )^{\underline {\rho +1}}}},

where $\Gamma$ is the gamma function. Thus, if $\rho$ is an integer,

f(k;\rho )={\frac {\rho \,\rho !\,(k-1)!}{(k+\rho )!}}.

The parameter $\rho$ can be estimated using a fixed point algorithm.^[2]

The probability mass function f has the property that for sufficiently large k we have

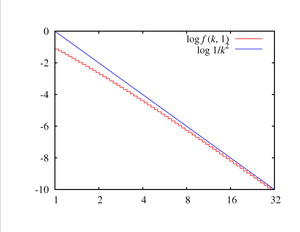
f(k;\rho )\approx {\frac {\rho \Gamma (\rho +1)}{k^{\rho +1}}}\propto {\frac {1}{k^{\rho +1}}}.

Plot of the Yule–Simon(1) distribution (red) and its asymptotic Zipf's law (blue)

This means that the tail of the Yule–Simon distribution is a realization of Zipf's law: $f(k;\rho )$ can be used to model, for example, the relative frequency of the $k$ th most frequent word in a large collection of text, which according to Zipf's law is inversely proportional to a (typically small) power of $k$ .

Occurrence

The Yule–Simon distribution arose originally as the limiting distribution of a particular stochastic process studied by Yule as a model for the distribution of biological taxa and subtaxa.^[3] Simon dubbed this process the "Yule process" but it is more commonly known today as a preferential attachment process. The preferential attachment process is an urn process in which balls are added to a growing number of urns, each ball being allocated to an urn with probability linear in the number the urn already contains.

The distribution also arises as a compound distribution, in which the parameter of a geometric distribution is treated as a function of random variable having an exponential distribution. Specifically, assume that $W$ follows an exponential distribution with scale $1/\rho$ or rate $\rho$ :

W\sim \operatorname {Exponential} (\rho ),

with density

h(w;\rho )=\rho \exp(-\rho w).

Then a Yule–Simon distributed variable K has the following geometric distribution conditional on W:

K\sim \operatorname {Geometric} (\exp(-W))\,.

The pmf of a geometric distribution is

g(k;p)=p(1-p)^{k-1}

for $k\in \{1,2,\dotsc \}$ . The Yule–Simon pmf is then the following exponential-geometric compound distribution:

f(k;\rho )=\int _{0}^{\infty }g(k;\exp(-w))h(w;\rho )\,dw.

The following recurrence relation holds:

\left\{{\begin{array}{l}kP(k)=(\alpha +k+1)P(k+1),\\[10pt]P(1)=\alpha B(\alpha +1,1)\end{array}}\right\}

Generalizations

The two-parameter generalization of the original Yule distribution replaces the beta function with an incomplete beta function. The probability mass function of the generalized Yule–Simon(ρ, α) distribution is defined as

f(k;\rho ,\alpha )={\frac {\rho }{1-\alpha ^{\rho }}}\;\mathrm {B} _{1-\alpha }(k,\rho +1),\,

with $0\leq \alpha <1$ . For $\alpha =0$ the ordinary Yule–Simon(ρ) distribution is obtained as a special case. The use of the incomplete beta function has the effect of introducing an exponential cutoff in the upper tail.

Bibliography

Colin Rose and Murray D. Smith, Mathematical Statistics with Mathematica. New York: Springer, 2002, ISBN 0-387-95234-9. (See page 107, where it is called the "Yule distribution".)

References

↑ Simon, H. A. (1955). "On a class of skew distribution functions". Biometrika. 42 (3–4): 425–440. doi:10.1093/biomet/42.3-4.425.
↑ Garcia Garcia, Juan Manuel (2011). "A fixed-point algorithm to estimate the Yule-Simon distribution parameter". Applied Mathematics and Computation. 217 (21): 8560–8566. doi:10.1016/j.amc.2011.03.092.
↑ Yule, G. U. (1925). "A Mathematical Theory of Evolution, based on the Conclusions of Dr. J. C. Willis, F.R.S". Philosophical Transactions of the Royal Society B. 213 (402–410): 21–87. doi:10.1098/rstb.1925.0002.

Probability distributions

List

Discrete univariate with finite support	Benford Bernoulli beta-binomial binomial categorical hypergeometric Poisson binomial Rademacher discrete uniform Zipf Zipf–Mandelbrot

Discrete univariate with infinite support	beta negative binomial Borel Conway–Maxwell–Poisson discrete phase-type Delaporte extended negative binomial Gauss–Kuzmin geometric logarithmic negative binomial parabolic fractal Poisson Skellam Yule–Simon zeta

Continuous univariate supported on a bounded interval	arcsine ARGUS Balding–Nichols Bates beta beta rectangular Irwin–Hall Kumaraswamy logit-normal noncentral beta raised cosine reciprocal triangular U-quadratic uniform Wigner semicircle

Continuous univariate supported on a semi-infinite interval	Benini Benktander 1st kind Benktander 2nd kind beta prime Burr chi-squared chi Dagum Davis exponential-logarithmic Erlang exponential F folded normal Flory–Schulz Fréchet gamma gamma/Gompertz generalized inverse Gaussian Gompertz half-logistic half-normal Hotelling's T-squared hyper-Erlang hyperexponential hypoexponential inverse chi-squared scaled inverse chi-squared inverse Gaussian inverse gamma Kolmogorov Lévy log-Cauchy log-Laplace log-logistic log-normal Lomax matrix-exponential Maxwell–Boltzmann Maxwell–Jüttner Mittag-Leffler Nakagami noncentral chi-squared Pareto phase-type poly-Weibull Rayleigh relativistic Breit–Wigner Rice shifted Gompertz truncated normal type-2 Gumbel Weibull Discrete Weibull Wilks's lambda

Continuous univariate supported on the whole real line	Cauchy exponential power Fisher's z Gaussian q generalized normal generalized hyperbolic geometric stable Gumbel Holtsmark hyperbolic secant Johnson's S_U Landau Laplace asymmetric Laplace logistic noncentral t normal (Gaussian) normal-inverse Gaussian skew normal slash stable Student's t type-1 Gumbel Tracy–Widom variance-gamma Voigt

Continuous univariate with support whose type varies	generalized extreme value generalized Pareto Tukey lambda q-Gaussian q-exponential q-Weibull shifted log-logistic

Mixed continuous-discrete univariate	rectified Gaussian

Multivariate (joint)	Discrete Ewens multinomial Dirichlet-multinomial negative multinomial Continuous Dirichlet generalized Dirichlet multivariate normal multivariate stable multivariate t normal-inverse-gamma normal-gamma Matrix-valued inverse matrix gamma inverse-Wishart matrix normal matrix t matrix gamma normal-inverse-Wishart normal-Wishart Wishart

Directional	Univariate (circular) directional Circular uniform univariate von Mises wrapped normal wrapped Cauchy wrapped exponential wrapped asymmetric Laplace wrapped Lévy Bivariate (spherical) Kent Bivariate (toroidal) bivariate von Mises Multivariate von Mises–Fisher Bingham

Degenerate and singular	Degenerate Dirac delta function Singular Cantor

Families	Circular compound Poisson elliptical exponential natural exponential location-scale maximum entropy mixture Pearson Tweedie wrapped

This article is issued from Wikipedia - version of the 11/4/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.